El otro día estaba en clase comentándole a mis estudiantes sobre la importancia de darle inteligencia a las máquinas. Evidentemente, no es el tipo de inteligencia que tenemos nosotros, sino más bien la capacidad para responder ante situaciones cambiantes y por supuesto, hacerlo de una manera eficiente y oportuna. Hoy en día, se les da inteligencia a las máquinas usando técnicas de inteligencia artificial, que han sido derivadas a partir de métodos estadísticos que nos permiten lidiar con la incertidumbre.

Les comentaba sobre los refrigeradores inteligentes que pueden entrar en modo ahorrador aprendiendo los patrones de uso, según las horas del día, si detectan luz o no, etc. Todas estas variables fluctuan en el tiempo y la máquina debe hacer una estimación a partir de la información de la que dispone sobre cómo será el uso en las siguientes horas. De esta manera, la máquina siempre se está adaptando al entorno y responde de la manera más eficiente posible.

Nosotros hacemos esto a diario, sólo que no lo hacemos de manera consistente y tampoco somos capaces de hacer valoraciones cuantitativas, pero las máquinas sí.

Quería comenzar esta discusión sobre las estimaciones y cómo lidiar con la incertidumbre presentando el famoso teorema de Bayes. El teorema de Bayes, o su implementación a veces llamada inferencia o razonamiento Bayesiano, nos permite ponerle números a nuestra certeza sobre un evento en particular. Además, nos permite actualizar nuestras creencias cuando tenemos nueva evidencia. Esto es extremadamente poderoso y quería discutirlo aquí con un ejemplo hipotético bastante ilustrativo inventado por Neil Manson.¹

Un soldado en combate

Imagina que eres un soldado en combate, estás metido en una trinchera. Sabes que del otro lado del campo de batalla a 400 metros queda sólo un soldado enemigo. Por una reunión previa de inteligencia, sabes que el ejercito enemigo está compuesto el 99% de soldados regulares y el 1% de francotiradores (incluso si no lo sabes puedes suponerlo, eso hacemos normalmente). Los soldados regulares son capaces de darle a un blanco a 400 metros el 20% de las veces, mientras que los francotiradores a esa misma distancia aciertan el 90% de las veces.

Así que tu te dices a ti mismo, probablemente sea un soldado regular. Pero para estar seguro, pones tu casco en un palo y lo asomas cuando ¡Bam! le dan al casco. Así que te preguntas, ahora que he visto esto, ¿será que es un francotirador? Bueno, tal vez fue un tiro de suerte de un soldado regular.

Pasan unos minutos y sacas nuevamente el caso, cuando ¡Bam! le dan nuevamente. Ahora ya más nervioso, comienzas a reevaluar tus creencias. Tal vez sí es un francotirador. Pero, ¿qué tan seguro puedes estas?

Bayes al rescate

Usaremos la notación establecida para hipótesis y datos: sea $\mathcal{H}_+$ la hipótesis (evento) que el soldado sea un francotirador, y $\mathcal{H}_-$ que no lo sea, esto es, que sea un soldado regular. De igual manera, sean $D_+$ y $D_-$ los datos positivos y negativos de una prueba, esto es, que un soldado dispare y acierte y que dispare y no acierte, respectivamente.

Se nos dan los siguientes datos,

$$\begin{align} &P(D_+\vert\mathcal{H_+})=0.9 \enspace, \\ &P(D_+\vert\mathcal{H_-})=0.2 \enspace, \\ &P(\mathcal{H_+})=0.01 \enspace. \end{align}$$

La primera expresión se lee, la probabilidad que al disparar acierte y sea un francotirador es del 0.9. Las siguientes de la misma manera. De estos datos podemos calcular los falsos negativos y los verdaderos negativos,

$$\begin{align} &P(D_-\vert\mathcal{H_+})=0.1 \enspace, \\ &P(D_-\vert\mathcal{H_-})=0.8 \enspace. \end{align}$$

La probabilidad que dispare no acierte y sea un francotirador es del 0.1. La siguiente de la misma manera. Todas la probabilidades se pueden visualizar como un arbol.

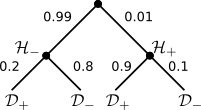
Entonces, la pregunta que debemos responder desde la trinchera es, ¿cuál es la probabilidad que sea un francotirador ($\mathcal{H_+}$) dado que ha acertado el disparo a mi casco $(\mathcal{D_+})$? El teorema de Bayes nos permite responder a esta pregunta, e incluso nos permite actualizar nuestras creencias según la evidencia que se nos presente en varias ocasiones. A continuación la ecuación de Bayes

$$\begin{align} &P(\mathcal{H_+}\vert\mathcal{D_+})= \underbrace{P(\mathcal{H_+})}_{\text{prior}} \frac{\overbrace{P(\mathcal{D_+}\vert\mathcal{H_+})}^{\text{likelihood}}}{P(\mathcal{D_+})} \enspace. \end{align}$$

Se lee la probabilidad que sea un francotirador dado que ha disparado y acertado. Esta es igual a la información previa (prior) de la que disponemos que los francotiradores son pocos (0.1) multiplicado por la posibilidad, también llamada “verosimiltud” (likelihood), que ocurra el evento. El numerador lo conocemos, la probabilidad que al disparar y acertar sea un francotirador $P(\mathcal{D_+}\vert\mathcal{H_+})=0.9$, pero debemos calcular el denominador, que es una especie de normalización. $P(\mathcal{D_+})$ es la probabilidad total que al disparar quien sea (francotirador o soldado regular) acierte. Esta se calcula de la siguiente manera

$$\begin{align} &P(\mathcal{D_+}) = P(\mathcal{D_+}\vert\mathcal{H_+})P(\mathcal{H_+}) + P(\mathcal{D_+}\vert\mathcal{H_-})P(\mathcal{H_-}) \enspace. \end{align}$$

Por lo tanto reemplazando los valores obtenemos lo siguiente

$$\begin{align} &P(\mathcal{H_+}\vert\mathcal{D_+})= 0.01 \frac{0.09}{(0.9)(0.01)+(0.2)(0.99)} = 0.0434 \enspace. \end{align}$$

De tal manera que, antes de sacar el casco creías que la probabilidad que ese único soldado fuera un francotirador era del 1%, mientras que después de sacar el casco una vez y al ver que acierta ha subido tu creencia al 4.3%. Esto no puede parecer mucho, y en primera instancia podríamos hasta creer que fue un tiro de suerte. Pero veamos lo que pasa cuando volvemos a probar la realidad una segunda vez. Esta vez usaré el teorema de Bayes, pero mi nuevo prior $P^{\ast}(\mathcal{H_+})$ será la probabilidad que acabo de calcular de 0.043

$$\begin{align} &P(\mathcal{H_+}\vert\mathcal{D_+})= 0.0434 \frac{0.09}{(0.9)(0.0434)+(0.2)(0.99)} = 0.165 \enspace. \end{align}$$

Ahora la probabilidad que sea un francotirador ha subido hasta el 17% aproximadamente, ¡3.8 veces!

Qué pasa si sacas el casco una tercera vez, pues la probabilidad sube hasta 0.428, así que concluyes que será mejor quedarte quieto y llamar por refuerzos porque estás seguro un 43% que ese tipo es un francotirador!!!